ここに、台所にあった3本のビンがある。

これらのビンを背の高い方から【A】【B】【C】と呼ぶことにする。
この3本のビンをテーブルの上に、適当な場所に置いてみる。

次に、ものさしを使って、【A】のビンの頭と【B】のビンの頭に当てる。

その時、ものさしがテーブルに当たる所に、青いシールを貼る。

これと同じことを、【A】と【C】、

【B】と【C】でもやってみる。

これで、3つのシールが貼れた。

この3つのシールは、どんな関係になっているか?
ものさしを当ててみると、直線になっていることがわかる。

3本のビンを適当に置いただけなのに、どうしてこうなるのか?
実は、ヒモを使うとよくわかる。
3本のヒモを、先ほど、ものさしを当てた位置で、つないでいく。

すると、3本のビンの頭で作られた三角形が見えてくる。
この三角形をヒモに沿って伸ばしていくと、

先ほどの青いシールの3つの点は、三角形の平面上にあることがわかる。
さらに、テーブルの下まで、三角形を伸ばしてみる。
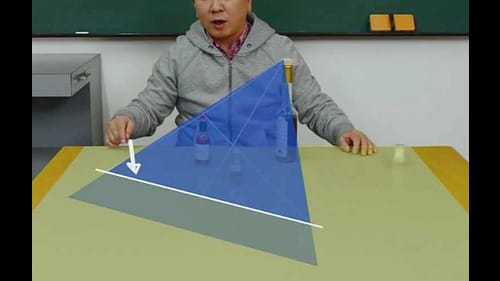
すると、三角形の平面と、テーブルの平面が交わる直線が見えてくる。
これは、平面と平面が交わる時、その交わる線は、必ず直線になるため。

先ほど、青いシールが直線に並んでいたのは、これが理由だった。






