アルミに包まれたチョコレート。

ここに、その大きさの違うチョコレートが3枚ある。

大きいもの、中くらいのもの、小さいもの。
これらは3つとも「正方形」で、厚さはどれも同じ。
まず、この3枚のチョコを大きいチョコと残りの2枚という2つのグループに分ける。

ここからが問題。
その2つに分けたチョコ、どちらか片方だけ食べていいと言われたらどちらを選ぶ?
当然、量が多い方がよい。
でも、見ただけでは、どちらの方が量が多いかわからない。
しかし、実は、重さや長さをはからなくても机の上に「ある置き方」をするだけで、どちらの方が量が多いか、正確に知ることができる。
いったいどうすればよいのか?
ここでは、「ピタゴラスの定理(※もしくは、三平方の定理)」を使う。
直角三角形のそれぞれの辺を「a」「b」「c」とすると、
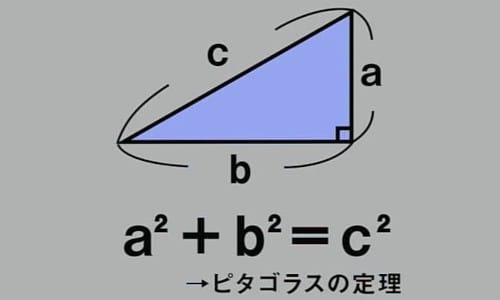
aの自乗とbの自乗を足すと、cの自乗になる という定理。
この定理の意味を考えるとこうなる。
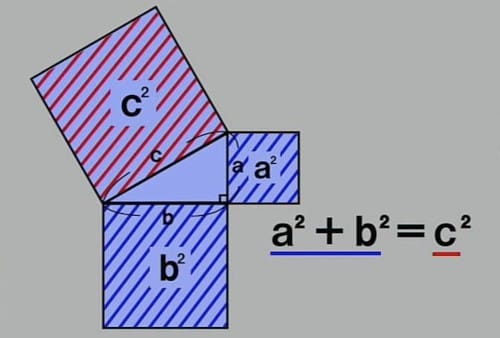
各辺を1辺とする正方形をかくと、1番大きな正方形の面積は、残り2つの面積を合わせたものと同じになる。
この3つのチョコでも、中くらいのチョコと小さいチョコを直角に並べた時、

もし、大きいチョコがここ(斜辺)にピッタリハマれば、ピタゴラスの定理により、大きいチョコと残り2つの合計は同じということになる。
しかし、大きいチョコを置いてみると、少しはみ出しているのがわかった。

つまり、大きいチョコ1枚は、残りの2枚を足したものより量が多いということになる。
このように、数学の定理を使うと並べるだけで物の大きさが比較できたりする。






