エラトステネスの篩(フルイ)〜100までの自然数の場合〜
ギリシャの学者エラトステネスは、地球の大きさを測った偉人。
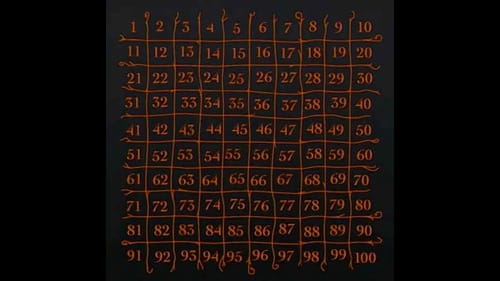
1を除く素数を並べる。
素数を見出すフルイにかける。
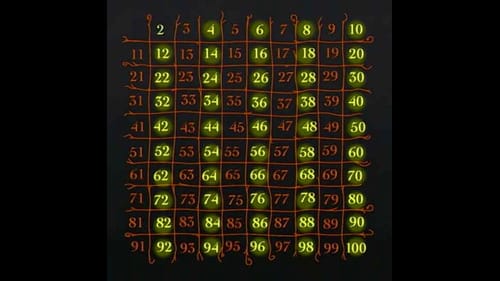
2の倍数を消す。素数の2はとっておく。
3の倍数を消す。素数の3はとっておく。
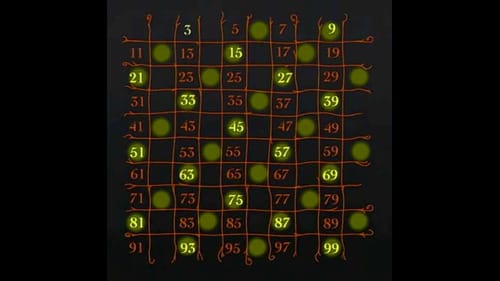
5の倍数を消す。素数の5はとっておく。
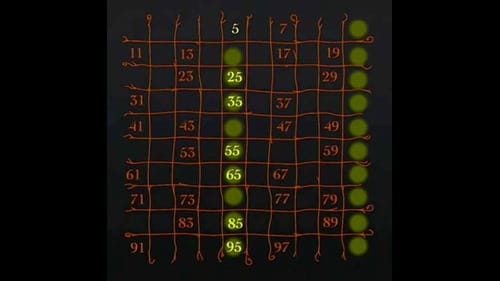
7の倍数を消す。素数の7はとっておく。
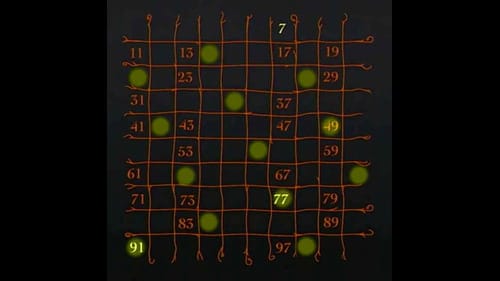
これだけで、100までの素数は見出すことができる。
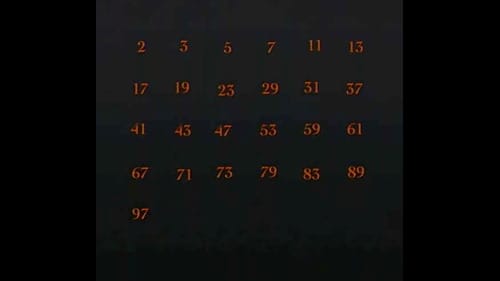
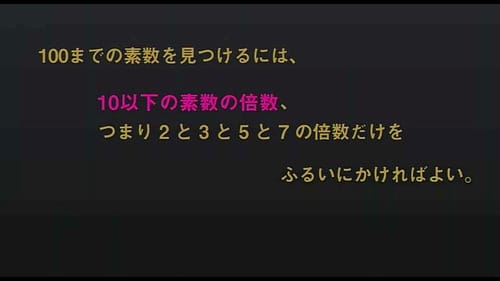
100までの素数を見つけるのに、
4つの素数 2、3、5、7の倍数だけをふるいにかけた。
なぜ、それだけでいいのか?