現代のラマヌジャン？素数の難問が夢に出てきたピラミッドで解けた？：探偵ナイトスクープ【2016/06/03】

素数の話です。

依頼内容

私は世界を驚かせる大発見をしました。
それは歴史上誰も解けなかった謎。
数学の素数の難問を解いてしまったのです。
私は子供の頃から不思議な夢を見てきましたが、およそ一年前、夢の中に素数の難問を解く鍵が突然現れたのです。
これは大発見以外の何ものでもありません。
数学は素人の私ですが、これが世に知られれば、現在日本では３人しか受賞していない数学界のノーベル賞とも言える「フィールズ賞」も夢ではないはず。
どうか世に発表する機会をいただけないでしょうか。

調査開始

依頼者の話によると、↓こちらの素数の本を読んで唯一わからないのが、

↓こちらの赤線が引いてある箇所だという。

例えば、ｘ＝２の場合、４から９の間に素数があるかということになる。この場合、５、７の素数が当てはまる。
この式に当てはめて、２つの数字間に素数が必ずあるということを証明できればすごいことだという。

そして、夢の中で出てきたヒントというのがこちら、立体のピラミッド。壁面には斜めや、バッテンなどの傷がついていたという。これは一体何なのか？

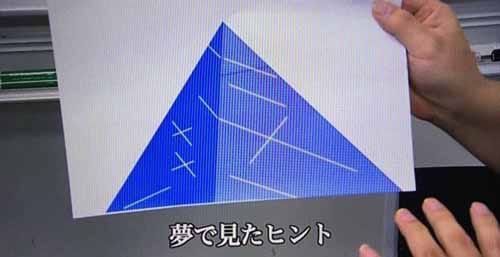
それを実際に模型で作ってみた。

で、さらにこのピラミッドを右下の方にずらして押してみた。

実は、この模型のそれぞれの階の板の裏には、１から順番に数字が書いてある。そして素数は黄色で塗りつぶしている。

今度は裏返したまま、ピラミッドを作って、隅に寄せてみることに。
そして、その素数をつなげてみると斜めに繋がる箇所がいくつか現れるのがわかった。これがさきほどのピラミッドの傷だったのです。

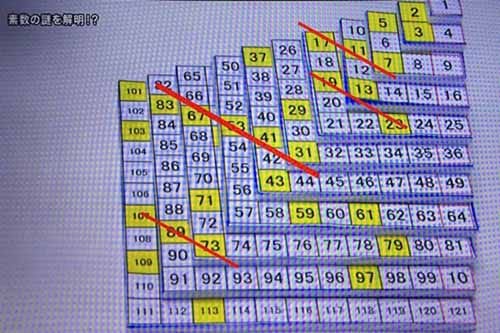
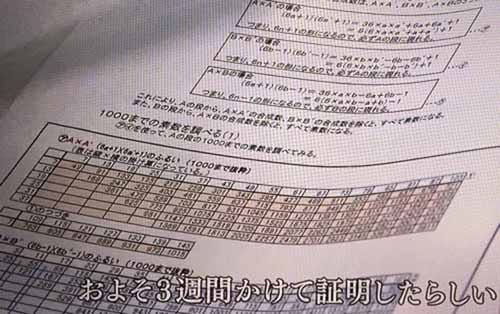
そして、夢をヒントに３週間かけて証明をしたらしいです。

数学の専門家たちに見てもらう

数学の専門家たちに集まってもらって見てもらうことになりました。

その中には、先ほど登場した本の著者もいました。

専門家たちによると、依頼者の証明には数学的に不完全な部分があった。

しかし、このピラミッドの形は専門家たちも見たことがないものだった。

さらに調査してみると、１９３２年にアメリカの学者クローバーが提唱した考え方と同じだったという。

もしこれより早く見つけていれば、「依頼者名のピラミッド」っという名前がついたんじゃないかという話も出た。

数学界では有名な話で、インドの魔術師と呼ばれる、天才数学者「ラマヌジャン」という人がいて、夢の中で女神様に問題を教えてもらって、それで公式を発見する人がいたという。

依頼者は現代のラマヌジャン？

表をJavascriptで表示してみた。

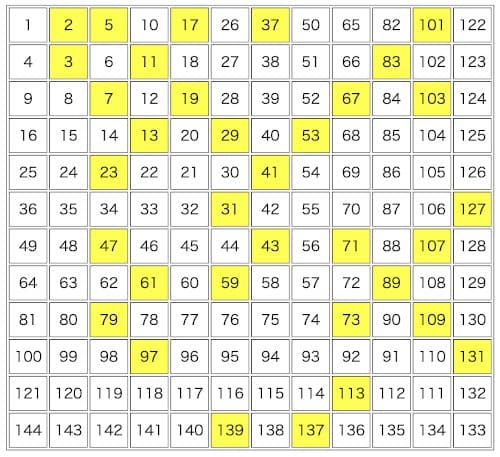
おもしろそうなので、ピラミッドで書かれていた表をJavascriptで作ってみました。
テーブルタグの都合で、左右反対になっております。
確かに規則的に斜めの線が入っているようにも見えますね。

↓ソースコードはこちら。