依頼内容
この間行われたワールドカップ最終予選。日本対タイの戦いをテレビで観戦していた時の話です。
大学の寮で、演劇部仲間のつのだ君と一緒に見ていたのですが、試合が始まってそうそう彼が、「せっかくだしゲームをしよう!」と言い出したのです。
そのゲームとは、試合に勝ったチームのみ得点を入れた選手の背番号を足していき、合計が偶数になるか奇数になるかを当てるというものです。
予想が外れた方は部屋を1人で掃除する罰ゲーム付き、僕は奇数を選び、つのだ君は偶数を選びました。
その時、友人のなりた君も合流、彼にゲームのルールを説明すると、「そんなの圧倒的に偶数が有利やん!」と言い出したのです。
結果は2対0で日本の勝利。ゴールを決めたのは、背番号8番の原口選手と、背番号18番の浅野選手。
二人の背番号を足すと26となり、結果は偶数。僕は、なぜ成田君は偶数が有利と思ったのか気になり、彼に尋ねると、独自の「成田理論」を熱く熱く語りだしたのです。
その理論は聞けば聞くほど、確かに偶数が有利だと思えるのですが、それでも僕はずっとモヤモヤしています。
探偵さん、本当になりた理論は正しいのか、このモヤモヤを取り払い、僕の疑問を解決してもらえませんか?お願いします。
成田理論
成田くんが言うには・・・
二人で、1得点づつを入れた場合の組み合わせパターンは3通りなので、偶数が確率的に有利。

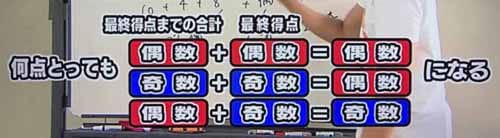
偶数と偶数=偶数
奇数と奇数=偶数
偶数と奇数=奇数
でも、サッカーはいつも2点で勝つとは限らない。
もし、4得点入れた場合はどうだろう?
10 + 4 + 9 = 23 (最初の3人の合計が奇数の場合)
10 + 4 + 9 + 偶数 = 奇数 (4人目が偶数の場合)
10 + 4 + 9 + 奇数 = 偶数 (4人目が奇数の場合)
10 + 4 + 8 = 22 (最初の3人の合計が偶数の場合)
10 + 4 + 8 + 偶数 = 偶数(4人目が偶数の場合)
10 + 4 + 8 + 奇数 = 奇数(4人目が奇数の場合)
となり、
何桁足し算しても、結局はその3パターンになるという考え。
しかし、ここでつのだ君がひらめいた。
偶数+奇数は奇数だが、逆にした、奇数+偶数も奇数なのではないか?
なので全部で4通りになり、確率は半々では?

でもこれは、成田理論の範疇だという。
偶数<>奇数 と入れ替えられるなら、偶数<>偶数、奇数<>奇数もそれぞれ入れ替えれるということになる。
偶数になる確率は、6通りのうちの4通りなので、偶数が有利なのは変わらない。
そこで、サッカー日本代表の過去100試合の統計を見てみると、奇数は39、偶数61となった。
数字さえあれば成田理論は通用するということね。
丁半博打で絶対勝てる?
だとすると、丁半でかけるサイコロ賭博で勝てるのでは?
そこでまた、つのだ君がひらめいた。
出目の合計のパターンを見てみると、偶数は6個に対して、奇数は5個。

これだけを見ると、圧倒的に偶数が有利に思えますが・・・。
山田先生の解説!
本当に成田理論が正しいのか、山田先生が解説してくれました。
・サイコロの罠
これはね、素人が陥りやすい罠なんですよ。
サイコロの出るパターンは、1つに対して6通りなので、36通りですよね。
足し算した結果を用意してみたんですよ。
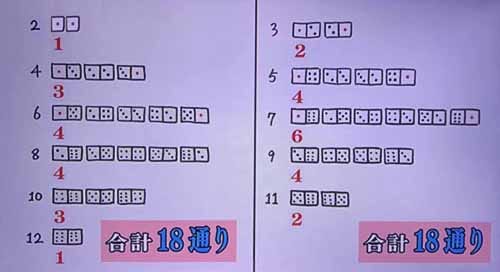
偶数が出るパターンが18通り、奇数が出るパターンも18通りなんですよ。
組み合わせの数が違うんですよ。
・サッカーの罠
2人で1得点づつ入れるパターンは、結局4通りなんですよ。


偶数<>偶数、奇数<>奇数を入れ替えることは、そもそもありえないということ。
結論:成田理論は崩れました。
再びスタジオ
たまたまですが、サッカーで得点を取る人の背番号は、偶数が多かったらしいです。





