数学者の吉永正彦 先生が、超平面配置の説明をしていました。
超平面配置とは?
あるものを1次元低い空間などで区切る場合、どのようなパターンがあるかを研究する数学のテーマ。
これだけの説明だといったい何のことを言っているのかよくわかりません。
例えば、
ネギ(1次元)に、4回包丁を入れると、最大5個に分かれます。

昆布(2次元)に、4回包丁を入れると、最大11個に分かれます。

豆腐(3次元)に、4回包丁を入れると、最大15個に分かれます。

これを表にしたものが、↓こちら。
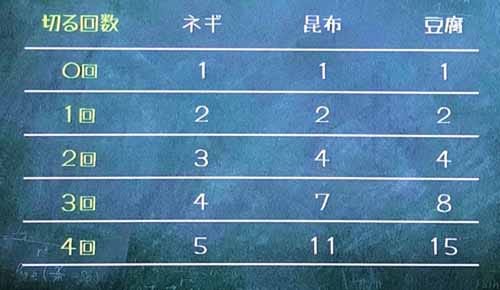
この表には、規則性があります。
例えば、全ての「切る回数」で、ネギと昆布を足した数が、1つ多い回数の昆布の数になっています。
そして、昆布と豆腐を足した数が、1つ多い回数の豆腐の数になっています。
さきほどの食材に包丁を入れるというのは、空間に何枚か超平面を配置した時に、その空間がいくつのピースに分かれるかというもの。
ある超平面配置の部屋の数を知りたい場合、1枚少ない場合の部屋の数と1次元低い場合の部屋の数を足すと求められる。
これを「加除原理」といいます。





